論文 “Quantum algorithm for dynamic mode decomposition integrated with a quantum differential equation solver” がPhysical Review Research誌に掲載
論文 “Quantum algorithm for dynamic mode decomposition integrated with a quantum differential equation solver” が,2024年10月11日付でアメリカ物理学会の学術論文誌Physical Review Research誌に掲載されました.https://doi.org/10.1103/PhysRevResearch.6.043031
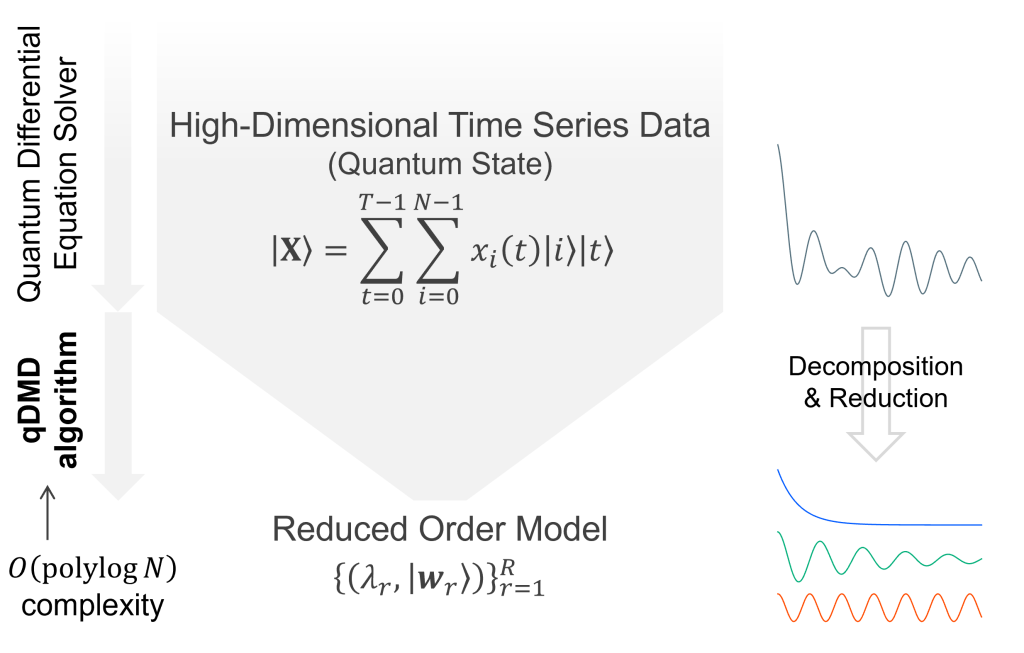
本研究において我々は,量子コンピュータ上でシミュレートされた時系列データを解析する汎用量子アルゴリズムを開発しました.水や空気の流れ,化学反応をはじめとする分子の運動,さらには感染症の流行などの動的現象は,微分方程式でモデル化されれます.微分方程式の数値シミュレーションは量子コンピュータの応用先としても期待されており,微分方程式を量子コンピュータ上で解くアルゴリズムの研究は多くあります.それらの量子アルゴリズムは微分方程式の解(i.e., 時系列データ)の情報を埋め込んだ量子状態を量子コンピュータ上で生成します.この量子状態に埋め込まれた時系列データの全部を古典コンピュータ上のデータとして取り出そうとすると,膨大な時間がかかることがこれまで問題とされてきました.本研究では,量子コンピュータ上でシミュレートされた時系列データに対して,量子コンピュータ上で動的モード分解とよばれる汎用時系列解析法を適用し,動的現象の理解に本質的な情報を古典コンピュータ上に取り出す汎用アルゴリズムの開発に成功しました.動的モード分解は,時系列データを,正弦的振動や指数関数的減衰,あるいはそれらを合わせた減衰振動といった基本的な時系列パターンの和に分解します.この時系列解析法は,流体力学や分子動力学などの多くの分野で有効性が示されているほか,動的現象の本質を表す縮約モデルの構築とそれに基づく現象予測や制御への応用可能性も示されています.我々が提案した量子動的モード分解(qDMD)アルゴリズムは,時系列データの次元Nに対して,計算量がlogNの多項式程度で済みます.一方で,既知の古典アルゴリズムでは,少なくともN程度の計算量が必要になります.つまり,我々の量子アルゴリズムはこの点において指数加速を実現しています.この研究成果により,流体力学や分子動力学などの大規模動的システム解析への量子コンピュータ応用の進展が期待されます.
本研究は,JSTさきがけ「量子情報処理」領域での研究課題「離散的化学反応論のための量子計算技術」(2020-2023年度,Grant Number: JPMJPR2018)において得られたものです.本研究成果を核に,現在進行中のJSTさきがけ「未来数理科学」領域での研究課題「作用素論的力学系解析のための量子計算技術」(2024年度-2027年度, Grant Number: JPMJPR24KA)において,量子コンピュータを用いた汎用動的現象解析ソフトウェアの研究開発を進めていきます.

